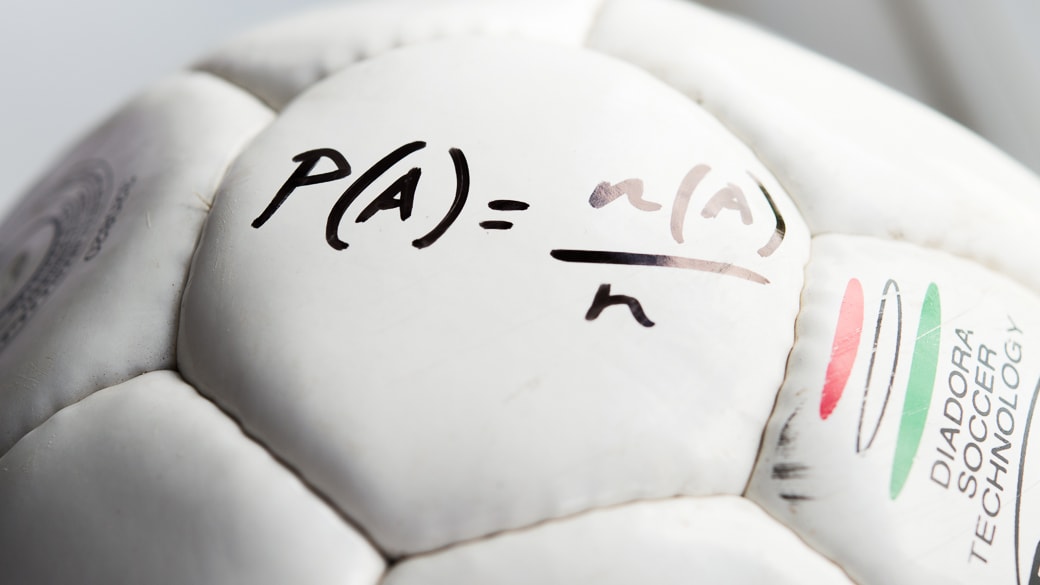The Maths behind the 50million.uk football competition

Introduction

As part of their campaign for Britain to leave the EU, Vote Leave are running a competition based around the upcoming Euro 2016 football tournament. This comes with an eye-popping prize of £50 million, supposedly the sum Britain gives to the EU every day. To win the prize, participants must correctly guess the outcome (win, lose or draw) of all 51 games in the tournament.

The following is a politically neutral attempt to look solely at the Maths behind this specific contest, and to analyse whether this is at all likely to be won.

(Some of) the Mathematics behind the 50million.uk contest

Introduction

I first came across this contest a couple of days ago, and instantly had a strong reaction of “something about this doesn’t add up”. As you can probably guess from the tongue-in-cheek title, the odds of someone winning £50 million through this contest are extremely small. (Although with an entrance fee of zero and a realistic prize of £50,000, this is still arguably a good deal).

Wanting to prove this, I got the calculator on my phone out to run some calculations on the train to work. The Maths behind this contest is largely at no higher a level than that taught in Year 8 in UK state schools, and certainly no higher than GCSE. Hopefully this shouldn’t be too tricky! If you’re not interested in the Maths / theory sections and want to get straight to the amusingly small numbers then you’re very welcome; just don’t expand these sections.

1. What are the odds of your guessing the correct outcome of a football match?

So, you’re sitting down to predict your Euro 2016 results. You think you really know your stuff about football, and think you’ve got a great chance of pulling this off. Let’s use some simple probability to explore your likelihood of winning.

Firstly, how confident are you of getting the outcome (win, lose or draw) of just one game correct? 50%? 70%?

(If you’re smart, you might say “it depends on the game!”. You’d be right – more on this later).

For now, let’s make the assumption  that you are a bonafide football genius, and you have a 4 in 5 (80%) chance of getting the result correct. In layman’s terms, this means that if the match was played 5 times, you would expect your result to occur 4 times. (These odds are extremely high, being about 30% higher than the running success rate of a bookmakers in a typical year. More on this later).

I’ve put the next two sections on probability theory in pop-out boxes. If you are already confident with calculating probability, or if you just want to get to the bit with the amusingly large numbers, then feel free to skip this bit.

[bs_collapse id=”collapse_7eca-7df6″]
[bs_citem title=”2. Theory part 1: using simple coin tossing to understand theoretical probability” id=”citem_998b-873c” parent=”collapse_7eca-7df6″]

2. The theory: using simple coin tossing to understand theoretical probability

Let’s take things back a bit.

To understand the likelihood of getting the outcome of 51 matches correct, we need to take things back a bit. Let’s look at a very simple situation: the flip of a coin.

The odds of getting heads on a coin are ½. This means that if you tossed 2 coins, you would expect 1 to land on the head.

We calculate the odds of two independent events happening by multiplying the odds of each event happening together.

P(2 heads) = P (Heads) x P (Heads) = 1/2 x 1/2 = 1/4.
[/bs_citem]
[bs_citem title=”3. Theory part 2: guessing the outcome of the group stage correctly” id=”citem_fff4-f60d” parent=”collapse_7eca-7df6″]

3. Applying the theory (part 1): guess the outcomes of the group stage correctly

Let’s take this further now, and try to predict the odds of guessing all the results in just one of the Euro 2016 groups.

Using your 80% odds from before, and our new knowledge about probability, let’s work it out.

Firstly, what are the odds of predicting two outcomes correctly? (We’ll keep things in percentages to keep the numbers simpler. 4/5 is the same as 80%).

As before:

[bs_well size=”md”]

P (two outcomes correct) = 80% x 80% = 64%.

[/bs_well]

That doesn’t look good! We’re already down from being 80% sure to 64% sure after just two games. What about three games?

[bs_well size=”md”]

P (three outcomes) = 80% x 80% x 80% = 51.2%

[/bs_well]

Oh no! That means our odds of guessing the outcomes of just three group games correctly are just over half. Hopefully this gives you a better understanding of how much the numbers can be against you in gambling.

Now, to correctly predict the outcome of every game in just one group, we would need to guess the outcome of six matches correctly. That is found by the following:

[bs_well size=”md”]

P (six outcomes) = 80% x 80% x 80% x 80% x 80% x 80% = 26.2% (roughly).

[/bs_well]

In other words, even our theoretical football genius only has odds of just over 1 in 4 of getting the outcomes correct for just one of the groups.

Now, there are six groups, each with six games. Writing out the above will take a whole lot of space, so I’m going to simplify things slightly:

[bs_well size=”md”]

Another way of saying 80% x 80% x 80% is 80%³ .

[/bs_well]

Similarly, another way of writing 80% x 80% x 80% x 80% x 80% x 80% is 80%⁶ n. If you want to follow on a calculator, look for a button saying “x^y“.

Using the above knowledge of calculating probabilities, we can now work out the odds of our genius correctly predicting all group stage results as:

[bs_well size=”md”]

80%³⁶ = about 0.000324%.

[/bs_well]

As a fraction, this is about 3 in a million. In other words, if 1 million people played 50million.uk, only 3 would be expected to guess all the outcomes for the group stage alone. (This is before the knockouts, guessing third place progressions or anything else, and using a very high chance of success for each individual game).

To put this number into perspective, in 2003 the Guardian listed the following events as being open for bets with a probability of less than one in a million:

• Prince Charles marrying Camilla, renouncing his right to be King, and then becoming an MP for the Green Party.
• Arnold Schwarzenegger becoming President of the US, then introducing compulsory German lessons in school.
• Tony Blair left Labour for the Conservative party, and becoming the first person to be Prime Minister for two different parties.

4. Apply the theory part 3: how hard is it to win the 50million.uk football contest?

Hopefully the terminology is now making sense to you, and we can speed things up a bit. There are 51 games scheduled for the Euro 2016 tournament. The odds of our genius guessing every one correctly are as follows:

[bs_well size=”lg”]

80%⁵¹ = (about) 0.0000114%.

In other words, roughly 1 in 10 million. Again, this is calculated for a very high ratio, without considering any further complications!

[/bs_well]

5. Theory vs practice

Let’s try and incorporate a few further factors.

Firstly, as already mentioned, I believe that my earlier stated 80% odds of predicting a result are far too high.

Mark Lawrenson, a football commentator for the BBC, writes a weekly column on the BBC football website where he predicts the outcome (win, lose or draw) for each of the upcoming weekend’s Premier League games, usually against a celebrity. These statistics provide an excellent comparison.

Firstly, he is someone who is professionally employed to speculate on such matters. Secondly, the BBC release all results in detail. Thirdly, his results for the 2012-13 season (a season I’m picking as I can link to a credible source in the BBC website) were better than the bookmaker’s, meaning that he can fairly be called someone who knows what he is talking about.

But what was his success rate for the 2012-13 season? Substantially worse than our hypothetical expert, down at 52.77%. If this seems low, again, it was better than the bookmakers that season. The purely theoretical odds of predicting an outcome of a football match are 1 in 3, or 33.3…%, and so to be almost 20% up on this is actually a strong achievement.

So, what would Mark Lawrenson’s odds of winning the 50million.uk game be (assuming he could keep this success ratio up)?

[bs_well size=”lg”]

52.77%⁵¹ = (about) 0.000000000000007%. In other words, this is roughly 7 in 100 quadrillion, an extremely small number.

To put the sheer tiny-ness of this number into context, imagine if the entire population of Earth (7 billion) were to play the game at these odds, with the same track record as Mark Lawrenson. The odds of ANYONE winning would be about 0.005%.

[/bs_well]

If you’re keener than me, you can find out much more on Mark Lawrenson’s success rates via this link.

6. Extending the problem

Apply findings to T&Cs

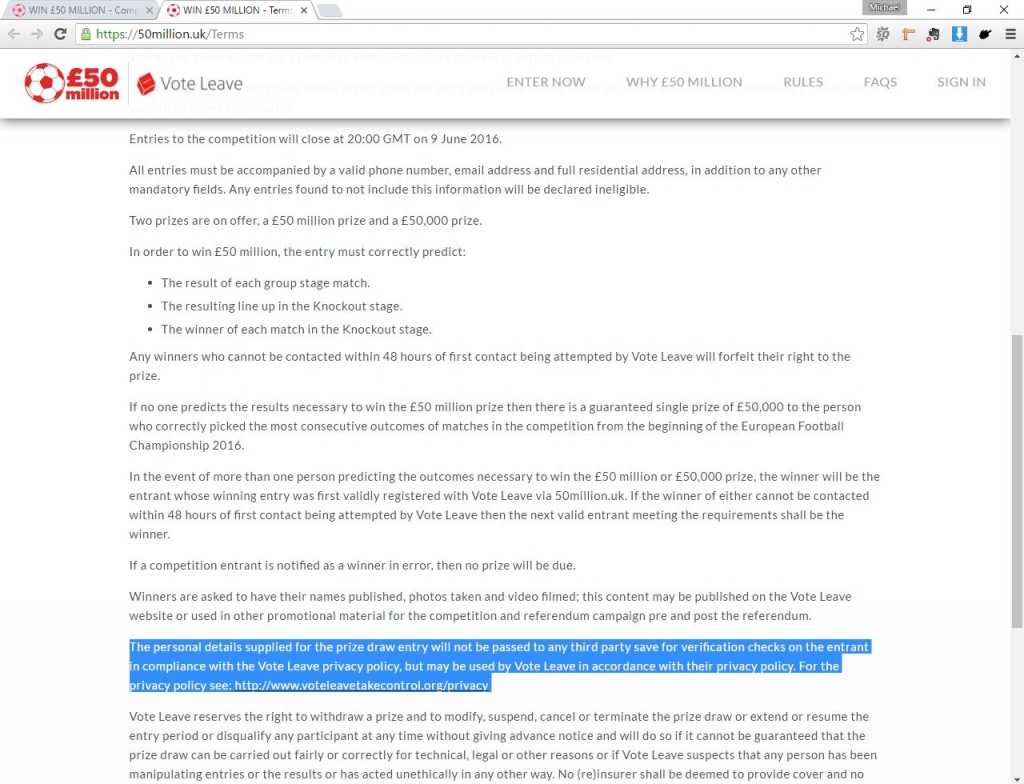
Let’s look at the terms and conditions from 50million.uk to see if we’re meeting everything required.

The sharp-eyed amongst you will spot that there are three conditions to have won the competition:

“In order to win £50 million, the entry must correctly predict:

• The result of each group stage match
• The resulting line up in the Knockout stage
• The winner of each match in the Knockout stage”

We’ve met point 1 and point 3, but arguably not point 2, as we haven’t factored in the likelihood of the player correctly guessing the order of teams in the group stages. I’m not going to get into the statistics of this here, but for argument’s sake let’s assume that this makes things comfortably more difficult.

7. The £50,000 prize

[bs_well size=”lg”]”If no one predicts the results necessary to win the £50 million prize then there is a guaranteed single prize of £50,000 to the person who correctly picked the most consecutive outcomes of matches in the competition from the beginning of the European Football Championship 2016.”[/bs_well]

Some good news at last! There is a 100% chance of someone winning the not-insignificant sum of £50,000 (albeit a prize one thousand times smaller than than the headline of the website would imply). The key term here is “the most consecutive outcome of matches in the competition from the beginning”. If we assume that 330,000 people register to play the game (which would be a large uptake for this kind of event), then the likely outcome is one person correctly predicting every outcome from the group section. In other words, focus especially hard on predicting the group stage games!

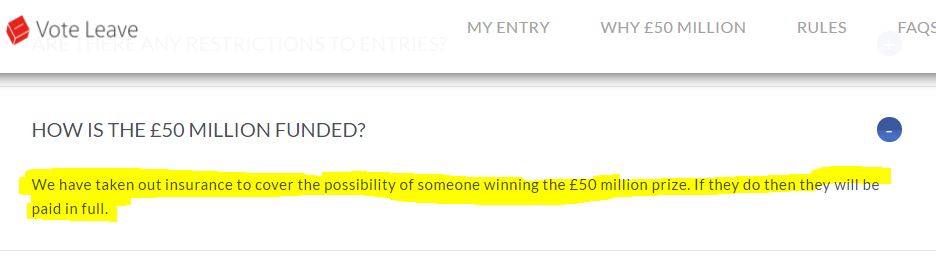
8. Do Vote Leave think anyone will win?

The fact that this prize is offered via an insurance policy with Lloyds of London suggests that both Vote Leave and Lloyds are relatively confident that this contest is unlikely to yield a £50 million prize.

Vote Leave have been clever here. This contest is costing them a definite £50,000, plus whatever they paid for the insurance policy (certainly less than £50 million), so whatever happens they will likely gain a large amount of exposure for a limited cost.

8. Further reading

FIFA rankings table

Link here

An interesting extension of the above model would be to assign higher chances of success to matches where there is a large gap in the FIFA rankings than to those where teams are more evenly matched. For example, Portugal (8th) vs Iceland (34th) (14th June, Group F) is the match with the highest differential in the FIFA rankings (a 26 ranking difference). This is arguably easier to call than Wales (26th) vs Russia (29th), with a difference of just 3 ranking places.

“The Black Swan”, Nassim Nicholas Taleb

Link here

Not really related to football, but for an example of the dangers of applying elementary statistics to events that are prone to extreme outcomes (e.g. wealth) this is hard to beat.

How to take part

Registration

To sign up, simply visit the website here [bs_button size=”md” type=”default” value=”Vist 50million.uk” href=”https://50million.uk/”].

[bs_well size=”sm”]The 50million.uk homepage[/bs_well]

How to play

Pick results

Now, the interesting bit! You firstly have to guess the outcome of every game in the group stages. This means predicting either who will win, or a draw, for every match. The interface makes this very quick and easy. (I also apologise here for my appalling choices!).

Pick table placings

Note the little drop down boxes in the tables above the results for each group. The tables automatically calculate group placings based on inputted results for each match. However, as the predictions don’t go into scores, there is no accounting for goal difference (the first factor used to distinguish teams finishing level on points). As a result, users have to guess the placings of teams finishing level on points. (This creates an added layer of mathematical complexity – more later).

Pick third place qualifiers

For the first time in this tournament, Euro 2016 is awarding qualification to the best four runners-up out of the groups. Accordingly, you have to pick the most likely teams to progress out of those that finish third in their groups. Again, this is something else that has to be predicted correctly, and again diminishes your odds of winning.

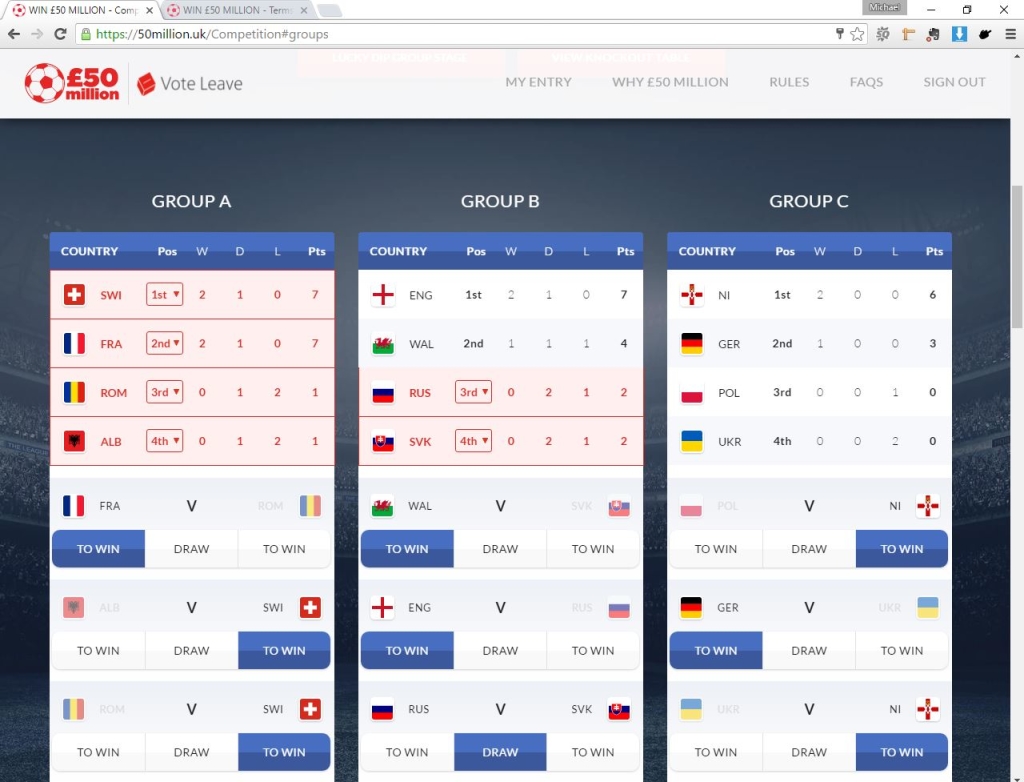
[bs_well size=”sm”]If the results go this well for England I’ll be happy…[/bs_well]

Pick knockout stage results

Once the group stages are all predicted is done, you then have to predict the outcome of each knockout stage game. As the name implies, there are now only two outcomes (winning or losing), down from three (win, lose or draw). The program is smart, and dynamically updates the teams in the next round based on the results you pick in the prior round. You have to follow through this process for the Round of 16, Quarter Finals, Semi Finals and Final.

If you’re interested, I’ve gone for an overall win for Germany. I’m also predicting a surprising run to the final from Switzerland, and semi-final heartache for England, along with a partial return to form for Spain in their reaching the Semi Finals. (At least if I’m right I’ll have £50 million in compensation). I’ve also gone for a home nations foursome in the quarter finals, which whilst I would love I can’t really see happening!

Submit details

At this point, you submit your details using a simple form, and you’re done. A final screen pops up saying thank you, before telling you several football related items you could buy with £50 million. (My favourite was 2 of Sunderland’s Stadium of Light, which seems like rather good value compared to half a Gareth Bale).

Note that in the Ts&Cs (more later), they explicitly mention needing the address to be correct for the prize to be collected.

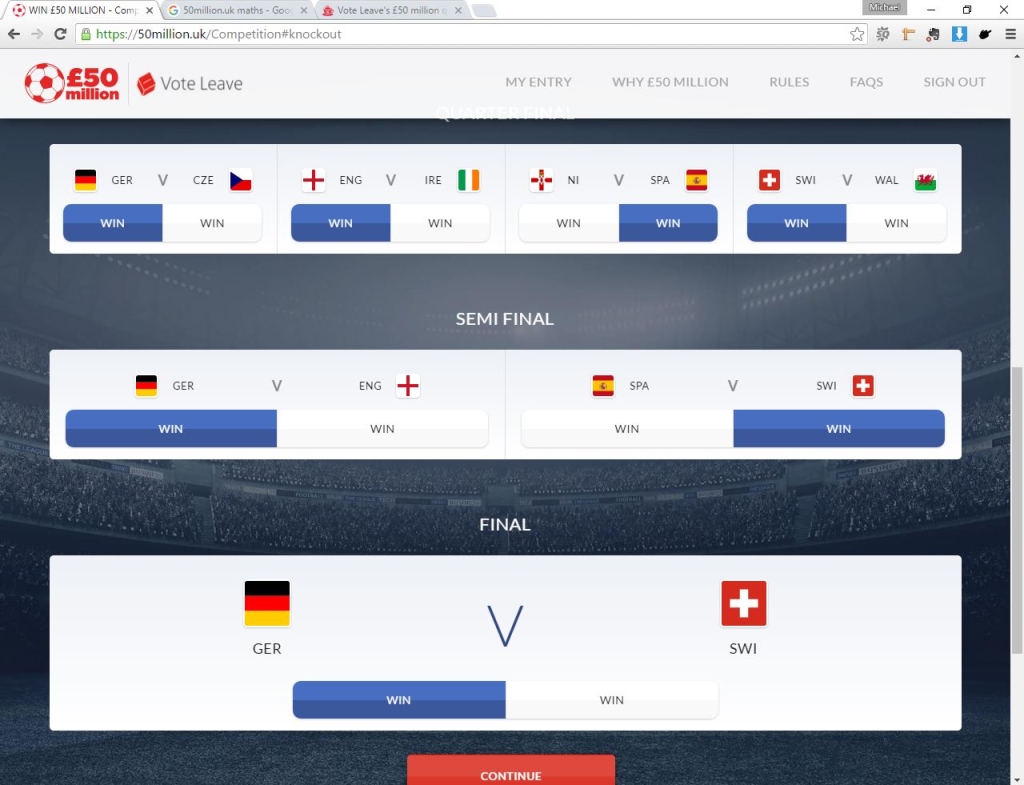
[bs_well size=”sm”]Predicting a German victory[/bs_well]